Metatron Dev. IV: ReSTIR

图片与部分证明来自Understanding The Math Behind ReSTIR DI

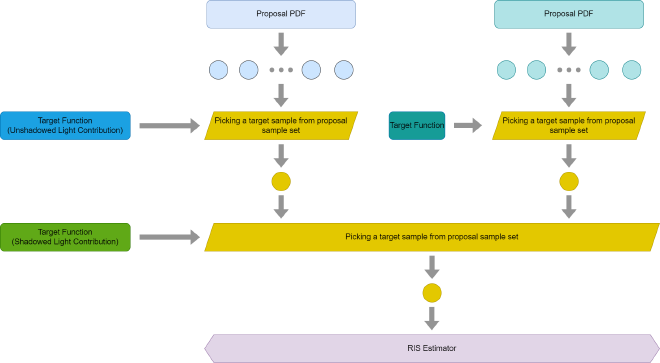
重采样重要性抽样
#

令$x$的目标概率分布为$\hat{p}(x)$, 它可能难以被重要性抽样. 我们为每个样本选择一个容易抽样的提议分布$p_i(X)$, 选出$M$个样本组成序列$\bold{x}$, 然后将每个样本的权重设置为$w_i(x_i)=m(x_i)\frac{\hat{p}(x_i)}{p_i(x_i)}$, 随机选择其中一个样本$x_z$, 此时概率如下.

$$ \begin{equation} \begin{aligned} p(z|\bold{x}) &=\frac{w(x_z)}{\sum_{i=1}^M w(x_i)} \end{aligned} \end{equation} $$

证明采用RIS进行Monte Carlo最终可以收敛的过程如下, 其中$y$为每次RIS所选择到的样本, $p’$为RIS后被选中的概率. 可以看出$\sum_{k=1,p_k(x) \neq 0}^Mm_k(x)=1$即可无偏. 由于目标概率分布被抵消, 不要求为积分为$1$, 渲染任务可选择Kajiya积分项为$\hat{p}(x)$.

$$ \begin{equation} \begin{aligned} E(\frac{1}{N}\sum_{i=1}^N\frac{f(y_i)}{\hat{p}(y_i)}\sum_{j=1}^Mw_j(x_{ij})) &=\frac{1}{N}\sum_{i=1}^NE(\frac{f(y)}{\hat{p}(y)}\sum_{j=1}^Mw_j(x_j))\\ &=E(\frac{f(y)}{\hat{p}(y)}W)\\ &=\sum_{k=1,p_k(x_k) \neq 0}^M\int\cdots\int\frac{f(x_k)}{\hat{p}(x_k)}Wp’(x_k)dx_1 \cdots dx_M\\ &=\sum_{k=1,p_k(x_k) \neq 0}^M\int\cdots\int\frac{f(x_k)}{\hat{p}(x_k)}W\frac{w_k(x_k)}{W}\prod_{i=1}^Mp_i(x_i)dx_1 \cdots dx_M\\ &=\sum_{k=1,p_k(x_k) \neq 0}^M\int\cdots\int f(x_k)m_k(x_k)\prod_{i=1,i \neq k}^Mp_i(x_i)dx_1 \cdots dx_M\\ &=\sum_{k=1,p_k(x_k) \neq 0}^M\int f(x_k)m_k(x_k)dx_k\int\cdots\int\underbrace{\prod_{i=1,i \neq k}^Mp_i(x_i)\underbrace{dx_1 \cdots dx_M}_{\text{M - 1, except k}}}_{1}\\ &=\int \sum_{k=1,p_k(x) \neq 0}^Mm_k(x)f(x)dx\\ \end{aligned} \end{equation} $$

蓄水池抽样
#

蓄水池抽样只保留一个样本, 样本保留的概率是当前样本的权重与所有已知样本权重和的比值. 蓄水池抽样更新过程如下. 保留新样本, 概率值为$\frac{w_i}{W}$; 保留旧样本, 概率值为$\frac{w_j}{W’}\frac{W - w_i}{W}=\frac{w_j}{W’}\frac{W’}{W}=\frac{w_j}{W}$. 可见概率值一定会更新为权重与已知权重和的比值.

Reservoir s, Sample sp, Weight w
s.W += w;
if u < w / s.W then
    s.y = sp;

若要合并多个蓄水池, 将每个蓄水池的权重和作为合并权重, 将蓄水池本身作为样本, 对多个蓄水池执行蓄水池抽样过程即可, 此时被选中的蓄水池中的样本的概率更新为$\frac{w_i}{W_j}\frac{W_j}{\sum_{k=1}^n W_k}=\frac{w_i}{\sum_{k=1}^n W_k}$, 仍然满足要求.

时空复用
#

空域复用具有不同的目标分布, 合并空域相邻蓄水池不可行, 需再次执行RIS, 将空域相邻的保留样本当作$1$个新样本添加到蓄水池, 提议分布为$\frac{\hat{p_i}(y)}{W}$, 目标分布与当前像素一致, 若为时域复用原理相同.

由于经历RIS后这是质量较高的样本, 我们选择将当前与相邻像素保留的样本添加到当前蓄水池$M$次, 因此被选中的概率提高$M$.

Reservoir s
for r in {r1, ..., rk} do
    s.update(r.y, p_hat(r.y) * r.W * r.M)
s.M = s1.M + s2.M + ... + sk.M

每个像素的RIS目标分布为未被遮挡的光照贡献函数, 而空间复用时需考虑提议分布的阴影遮蔽, 由于空域相邻的提议分布包含$\hat{p_i}(y)$, 在相邻像素执行阴影测试即可. ReSTIR原文通过该方法确定$m_k(x_k)$, 剔除遮挡样本保证无偏.

for qi in {q1, ..., qk} do
    if p_hat_qi(s.y) > 0 then
        Z += ri.M
m = 1 / Z

重采样重要性抽样#

蓄水池抽样#

时空复用#

重采样重要性抽样
#

蓄水池抽样
#

时空复用
#